원의 크기와 상관없이 원의 둘레와 지름의 비는 일정한데, 이 비를 원주율이라 하고 π로 나타낸다.
원의 지름이 1일때 원의 둘레의 길이는 1π. 즉, 3.14 이다.
왜 3.14일까?
*다각형의 둘레를 이용한 원주율의 근사값 계산.
원의 둘레는 내접정다각형의 둘레보다 크고 외접다각형의 둘레보다 작다. 이 사실과 외접원의 반지름의 길이가 1인 원의 둘레는 2π라는 사실을 이용하면 π의 근삿값을 구할 수 있다.
예를 들어, 반지름의 길이가 1인 원에 내접하는 정육각형의 한 변의 길이는 1이고 외접하는 정육각형의 한 변의 길이는 2/3√3이므로 6 < 2π < 4√3임을 알 수 있다. 이로부터 π는 3보다 크고 3.6보다 작음을 알 수 있다.
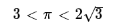
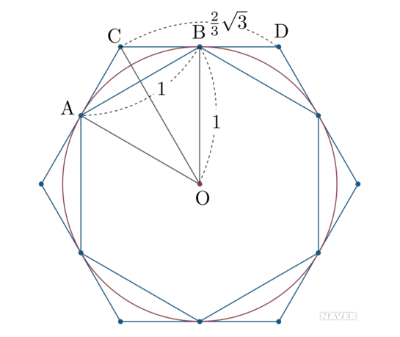
이러한 방법으로 다각형을 계속 쪼개어 변의 길이의 합, 외접하는 변의 길이의 합과 원의 둘레와 비교하면3.141592653589...의 무리수가 나온다.
정밀한 계산에서는 원주율을 3.1416 또는 3.14159로 계산하는데, 인공위성 등 첨단의 계산에서는 소수점 아래 30자리까지 계산된 원주율을 사용한다.
참고 [네이버 지식백과] 원주율
'::public > 수포자를 위한 게임 수학' 카테고리의 다른 글
| 사인과 코사인(Cin & Cos) (0) | 2019.11.14 |
|---|---|
| 라디안(Radian) (0) | 2019.11.14 |
| 벡터(vector) (0) | 2019.11.14 |
| 선형대수학(Linear Algebra) (0) | 2019.11.14 |
| 피타고라스의 정리(Pythagoream theoream) (0) | 2019.11.14 |



