크기와 방향을 가지고 있는 양으로써 두 가지 정보를 모두 표현할 수 있는 화살표로 나타낸다.
대응되는 개념으로 크기만을 가지는 변량은 '스칼라'이다.
즉, 길이, 질량, 넓이는 '스칼라'이고 속도, 가속도, 힘은 '벡터'이다.

*벡터의 합.


*좌표평면에서의 위치벡터.

*좌표평면에 나타낸 벡터의 크기.
;좌표평면에서 두 점 사이의 거리를 구할 때 피타고라스의 정리를 이용한다.
시점이 0이고 종점이 A(a1, a2)인 벡터의 크기도 피타고라스의 정리를 이용하여 구할 수 있다.
a = (a1, a2)일 때, 원점 0와 점 A(a1, a2)에 대하여 a = →OA이므로 벡터 a의 크기는 선분 OA의 길이와 같다.
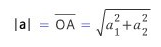
*좌표평면에 나타낸 벡터의 덧셈, 뺄셈.
좌표평면 위의 두 점 A(a1, a2), B(b1, b2)에 대하여 두 점의 위치벡터를 각각 a, b라고 하면 a = (a1, a2), b = (b1, b2)이므로 두 벡터의 합, 차, 스칼라 배는 각각 다음과 같이 대응되는 성분끼리 연산을 하면 된다.
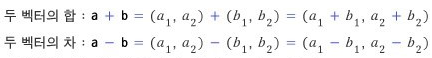
참고 [네이버 지식백과] 좌표평면과 벡터 - 벡터를 알아보자 (수학산책, 이광연)
*벡터의 내적 공식.
벡터의 내적을 구하는 공식이다. n차원 벡터의 경우 벡터의 좌표나 벡터의 길이와 사잇각을 이용하여 구할 수 있다.
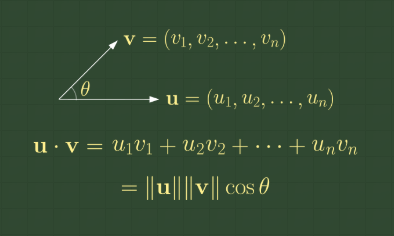
참고 [네이버 지식백과] 벡터 내적 공식 [scalar product] (자주 찾는 수학 공식)
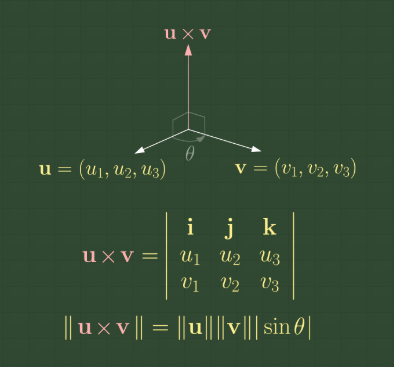
*벡터의 외적 공식.
두 3차원 벡터의 외적(=벡터곱)을 구하는 공식이다. u, v 두 벡터의 외적u × v는 벡터의 좌표를 이용하여 구하거나, u, v, u × v가 오른손계가 되고 길이가 u, v가 이루는 평행사변형의 넓이와 같도록 구하면 된다.
[네이버 지식백과] 벡터 외적 공식 [vector product] (자주 찾는 수학 공식)
'::public > 수포자를 위한 게임 수학' 카테고리의 다른 글
| 라디안(Radian) (0) | 2019.11.14 |
|---|---|
| 원주율π(파이, Pi) (0) | 2019.11.14 |
| 선형대수학(Linear Algebra) (0) | 2019.11.14 |
| 피타고라스의 정리(Pythagoream theoream) (0) | 2019.11.14 |
| 수포자를 위한 게임 수학_유투브 (0) | 2019.11.12 |



